Hareket Çeşitleri

a) Düzgün Doğrusal Hareket (DDH) (Sabit Hızlı = Süratli Hareket) (SHH) :
Bir cismin sürati hareketi süresince değişmeyip sabit kalıyorsa ve cisim bir doğru boyunca hareket ediyorsa cismin yaptığı bu harekete düzgün doğrusal hareket veya sabit süratli (hızlı) hareket denir.
Sabit süratli harekette;
• Cisim eşit sürelerde eşit yollar alır.
• Cismin sürati hareketi boyunca değişmeyip sabit kalır.
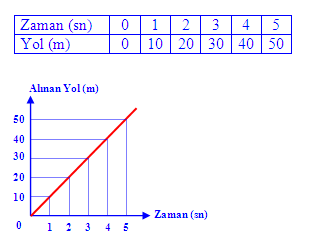
Yol – Zaman Grafiği :
Hareketli, hareketi süresince eşit sürelerde eşit yollar alır ve bu nedenle sürati sabittir.
Hareketlinin yol – zaman grafiğinden sürati bulunur. Grafikten seçilen her hangi bir noktanın zaman ve yol eksenlerini kestiği noktalar bulunur. Bu noktalara karşılık gelen değerler sürat formülünde yerine yazılarak sürat hesaplanır.

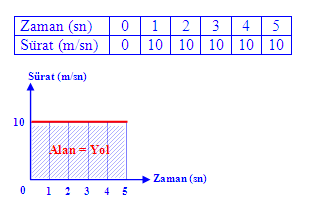
Sürat – Zaman Grafiği :
Hareketli, hareketi süresince eşit sürelerde eşit yollar alır ve bu nedenle sürati sabittir. Zaman değişse bile sürat değişmez.
Hareketlinin sürat – zaman grafiğinden aldığı yol bulunur. Sürat – zaman grafiğinin altında kalan alan hareketlinin aldığı yolu verir.

b) Düzgün Hızlanan Doğrusal Hareket (DHDH) :
Bir cismin hızı hareketi süresince eşit zamanlarda eşit miktarlarda artıyorsa ve cisim bir doğru boyunca hareket ediyorsa cismin yaptığı bu harekete düzgün hızlanan doğrusal hareket denir.
Düzgün hızlanan doğrusal harekette;
• Cismin sürati eşit sürelerde eşit miktarlarda artar.
c) Düzgün Yavaşlayan Doğrusal Hareket (DYDH) :
Bir cismin hızı hareketi süresince eşit zamanlarda eşit miktarlarda azalıyorsa ve cisim bir doğru boyunca hareket ediyorsa cismin yaptığı bu harekete düzgün yavaşlayan doğrusal hareket denir.
Düzgün yavaşlayan doğrusal harekette;
• Cismin sürati eşit sürelerde eşit miktarlarda azalır.

Sürat Birimleri

 Sürat :
Hareketli bir cismin belirli bir yolu ne kadar zamanda aldığını gösteren büyüklüğe sürat denir.
Bir cismin hareketi süresince aldığı toplam yolun, cismin toplam hareket süresine bölümüne sürat denir.
Bir cismin birim zamandaki aldığı yol miktarına sürat denir.
Bir cismin süratini, o cisme etki eden kuvvet etkiler.

BLAİSE PASCAL'IN HAYATI (19 Haziran 1623- 19 Ağustos 1662)

Blasie Pascal; Fransız matematikçisi, fizikçisi, felsefecisi ve yazarıdır. Akışkanlar yasalarından biri olan pascalı bulmuştur.
Clermont Vergi Mahkemesi başkanı olan babası iyi bir matematikçi ve bilgili bir kişiydi. Karısının ölümünden 5 yıl sonra ailesiyle birlikte Paris ‘e yerleşti. Fiziğe ve matematiğe duyduğu ilgiden dolayı dönemin tanınmış edebiyat ve bilim adamlarıyla bağlantı kurdu. Küçük yaşta gelişen yetenekleri sayesinde birlikte olduğu çevreye yabancılık çekmedi. Babasıda oğlunun bu yeteneklerini farkedince oğluna ders vermeye başladı.
Henüz çocuk denilecek yaştayken, Eukleides’in ilk 32 teorisini öğrenen, 11 yaşında sesler üstüne bir inceleme yazan (Tratie surles sons (sesler üstüne inceleme)) Blasie Pascal, 12 yaşına gelince kendi kendine geometri öğrendi. Daha sonra sesin hızını ölçen P.Mersone’in (1588-1648) düzenlediği bilginler arası toplantılara katıldı. Pascal 16 yaşında Desan ques‘in 1639’da izdüşümsel geometri kitabından esinlenerek Essai sur les coniques (konikler üstüne deneme) adlı yapıtını yazdı. 1639’da Rouen’da maliye dairesinde önemli bir göreve atanan babasıyla birlikte gitti, onun işlerini kolaylaştırmak amacıyla bir hesap makinesi tasarladı. Jansenusçula bağlandı. Bu arada Toriçelli’nin tüpler içinde sıvıların yükselmesi, havanın ağırlığı vb. üstüne deneylerini yineledi, boşluk konusunda çalışmalar yaptı. 1647’de “Boşlukla İlgili Yeni Deneyler” adlı incelemesini yayımladı. Boşluk incelemesine girişide bu dönemde yazdı.
1647’den sonra kız kardeşi jacquleline ile Paris’e yerleşmiş olan Pascal’ın sağlık durumu iyiden iyiye bozulmuştu. Doktorların önerilerine uyup gezip dolaşmaya, salonlara girip çıkmaya başladı, liberten kişilerle bağlantı kurdu.
1651’de babası ölmüş, kızkardeşiyle Port Royal Manastır’a gitmiştir. Pascal’ın monden yaşamı 1654’te sona ermişti. Çünkü fikirleri değişmişti. 23 Kasım 1654’te şiddetli bir diş ağrısı nedeniyle uykusuz geçen bir gecede sikloit eğrisi üzerinde düşünmeye başlayan Pascal, bunu izleyen sekiz gün içnde sikloite ilişkin önemli buluşlar ve Port Royal’a girişinden sonraki tek bilimsel çalışması “Sikloit Üzerine” (1658) adlı yapıtını yayımladı. Pascal “Hristiyan Dininin Savunması” adlı bir yapıt yayımlamayı düşünüyorken öldü.

DNA ÜZERİNDEKİ FOSFATIN ÖNEMİ

Fosfatlar, DNA üzerindeki nükleotid bazları birarada tutarlar. Çünkü DNA sarmalı su içeren bir ortamda işlev yapar ve su da fosfatlar ile şekerler arasındaki bağları parçalar. Bu bakımdan DNA üzerindeki fosfat gruplarının eksi yüklü olması hem bir avantaj hem de bir gerekliliktir. Bu eksi yük sayesinde DNA'nın bulunduğu sulu ortamda parçalanma ihtimali engellenmiş olur.
Fosfattan başka hangi bileşik bir yandan kimyasal bağ kurup, bir yandan da eksi yüklü kalmayı başarabilir diye sorulacak olursa, çeşitli ihtimaller vardır.
Ancak bunların hiçbiri genetik bilgiyi oluşturma özelliğini fosfat gibi gerçekleştiremez. Örneğin silisik asit ve arsenik esterler suda hızla parçalanırlar; sitrik asit ise suda daha yavaş parçalansa da, molekülün geometrisini sağlayacak kararlılıkta değildir.Dolayısıyla fosfatın kendine has özellikleri olmasaydı, DNA çifte sarmalı olmayacak, kendini kopyalayabilen bu biyokimyasal sistem kurulamayacak ve canlılıktan söz etmek mümkün olmayacaktı. Ünlü kimya profesörü Frank Henry Westheimer bu özel durumla ilgili "tüm bu koşullar ancak fosforik asit ile karşılanabilir ve görünürde başka bir alternatif de yoktur.''demektedir.

RAKAMLARLA HÜCRE

*Bir insandaki toplam hücre sayısı 100 trilyon
*Bir insandaki farklı hücre çeşitleri 210 kadar
*Her saniye ölen hücre sayısı yaklaşık 50 milyon
*Her saniye yeni yaratılan hücre sayısı yaklaşık 50 milyon

*Toplam alyuvar sayısı (eritrosit) 25 trilyon
*Toplam akyuvar sayısı (lökosit) 25-100 milyar arası
*Toplam sinir hücresi sayısı 30 milyar (Bir sinekte 100 bin, fare beyninde ise 10 milyon sinir hücresi vardır)
*Beyin kabuğundaki (korteks) sinir hücresi sayısı 10 milyar
*Beyincik korteksindeki hücre sayısı 10 milyar
*Bütün sinir hücrelerinin toplam sinaps sayısı 100 trilyon
*Normal hâlde günlük ölen sinir hücresi sayısı 50.000-100.000
*Bir hatırlama sürecinde faal olan beyin hücresi sayısı 10 milyon-100 milyon
*Mide asiti üreten hücre sayısı (erkekte) yaklaşık 1 milyar (kadında) yaklaşık 820 milyon
*En küçük hücre olan spermlerin boyu 3-5 µm
*Beyindeki glia hücrelerinin boyu 5 µm
*En büyük hücre olan yumurta hücresinin çapı 100-120µm
*Bir karaciğer hücresinin ortalama büyüklüğü 30-50µm

ARŞİMET’İN HAYATI

Eski Yunan matematikçi ve fizikçisidir. (Syrakusai M.Ö. 287-ay.y. 212) Genç yaşta öğrenimini tamamlamak ve ünlü bilim adamı Eukleides’ in derslerini izlemek üzere Antik çağın kültür merkezi olan İskenderi‘ ye gitti. Yer kürenin çevresini zamanına göre çok iyi bir yaklaşımla veren Eratusthenes ile tanıştı. Yurduna döndükten sonra kendini tamamıyla ilmi çalışmalara adadı. Matematik, fizik ve astronomi üzerinde çalıştı.
İlk olarak Arşimet daire çevresinin çapına oran olan pi sayısını,daire içine ve dışına çizilmiş düzgün çokgenler yardımıyla yaklaşıklıkla veren bir metot ortaya koydu. Çok büyük sayıları kolaylıkla belirtmeye yarayan bir yöntem bularak Yunan sayı sistemini geliştirdi. Yayların toplama ve çıkarma formüllerini buldu. Koniklerin (elips, parobol,hiperbol) kendi çevresinde dönmesiyle oluşan geometrik şekilleri inceledi. Arşimet ‘in mekanik alanda da başarıları vardır. Sonsuz vidanın hareketli makaranın, palanganın ve dişli çarkın bulucusu olarak tanınır. “Bana bir dayanak noktası gösterin dünyayı yerinden oynatayım” sözü Arşimet’e aittir.
Kurumsal çalışmaları yanında söylenceleşmiş pratik çalışmalarıda vardır. Bunlardan en ünlüsü Syracusa kralı ve dostu Hieron ‘un kendisi için yaptırdığı altın taca başka bir maden karıştırıldığından kuşkulanarak Arşimet ‘ten taç bozulmadan bunu ortaya çıkarmasını istemesiyle ilgilidir. Arşimet bu sorun üstüme düşünür, ancak birşey bulamaz. Bir gün hamamda yıkanırken suyun vücudunun batan bölümünün hacmiyle orantılı bir kuvvetle yukarı doğru ittiğini bulur. Bu yolla tacın saf altından yapılıp yapılmadığını düşünen Arşimet büyük bir sevinçle çrılçıplak olrak sokağa fırlamış ve bağırmıştır: Eureka, Eureka (buldum, buldum )…
Ayrıca Arşimet M.Ö. 215’te Konsal Marcellus komutasındaki Roma ordusuna karşı Syracua kentinin savunmasında yer aldı. Bu savunmada çok uzak mesafelere ok ve taş atan mekanik aletler yaptığı ve kurduğu ayna sistemiyle güneş ışınlarını Roma donanması üzerinde odaklayarak gemileri yaktığı söylenir. Herşeye rağmen Romalılar bir şans eseri Syracusa’ ya girdiler. Marcellus, askerlerine bu büyük adama iyi davranılmasını emretmiştir. Ancak Arşimet ‘I tanımayan bir asker bir problemin çözümüne iyice dalmış olan bilginin kendisine cevap vermemesi üzerine kızarak öldürdü.
Arşimet Prensibi : cisimlerin sıvı ya da gaz ortamlar içerisindeki denge koşullarını açıklayan, fiziğin temel ilkelerinden biridir.
Arşimet’in ortaya koyduğu bu ilkeye göre sıvı ya da gaz ortam içeresinde bulunan bir cismin ağırlığı, kendi hacmine eşit hacimdeki sıvının (gazın) ağırlığı kadar azalır. Eğer cismin yalnız bir bölümü sıvı (gaz) ortam içerisinde bulunursa ağırlığı kadar azalır. Buna göre hacmi V,ağırlığı G, ve yoğunluğu Q olan bir cismin sıvı (gaz)ortam içerisine kalan bölümün hacmi V, sıvının (gazın) yoğunluğuda Q ise cismin sıvı (gaz) ortam içerisindeki ağırlığı G=G-F’ dir. Böylece cismin ağırlığındaki azalmaya neden olan ve sıvı (gaz) tarafından yukarıya doğru etki ettirilen F kuvvetine kaldırma kuvveti denir. Bu kuvvet cismin, sıvı (gaz) içinde kalan bölümün hacmi kadar hacimdeki sıvının ağırlığına eşit olduğundan Arşimet ilkesi matematiksel olarak :
F=VQ-V’Q’=(V-V’)Q=V’Q’ Bağıntılarıyla gösterilir.
Arşimet ilkesinin ilginç sonuçlarından birisi, cismin sıvı ya da gaz ortam içerisinde bulunan bölümün hacmine eşit hacimdeki sıvı ya da gazı, bulundukları kaptan taşırmasıdır. Bu bakımdan kaldırma kuvveti, taşan sıvı ya da gazın ağırlığına eşittir. Bu olay, içinde su bulunan ölçekli bir kaba uygun bir cisim atılarak kolayca gözlenebilir.

Gregor Johann MENDEL' in Hayatı (1822-1884)

Avusturyalı rahip , botanik kalıtım bilgini.
Bitkiler üzerinde yaptığı incelemelerle kalıtımın temel yasalarını ortya koymuş ve kalıtım biliminin öncüsü olmuştur.
22 Temmuz 1822’de Silezya’daki Heinzendorf’ta (Bugün Çekoslavakya’da Hyncice) doğdu.6 Ocak 1884’de Moravya’daki Brünn’de (Bugün Çekoslavakya’da Brno) öldü.Çekce ve Almanca konuşulan Silezya’da yerleşmiş üç çocuklu bir ailenin tek erkek çocuğu olan Mendel ‘in babası çiftçi,annesi ise kuşaklar boyu bahçıvanlıkla uğraşan bir ailenin kızıydı.Daha çok küçük yaşlarda ,babasından bitki yetiştirmenin tüm inceliklerini öğrenen Mendel 1833’de Leipnik’teki , bir yıl sonra da Trappav’daki bir liseye gönderildi.Burada üstün başarısıyla dikkati çekince 1840’da lise diplomasını aldıktan sonra üniversite öğrenimine hazırlık amacıyla Olmütz Üniversitesi’nde felsefe derslerini izledi.Ailesinin kısıtlı ekonomik koşulları nedeniyle , bu kurumdaki iki yıllık eğitimini küçük kardeşi Theresia ‘nın çeyiz parasının bir bölümünü harcayarak sürdürebilen Mendel, 1843’te fizik profesörünün önerisiyle Brünn’deki Augustinus tarikatının manastırına girdi ve Gregordini adını aldı.1844-1848 arası bir yandan din eğitimini görürken, bir yandan da manastırın bilimsel araştırmaya önem veren yaklaşımından yararlanarak felsefe Enstitüsü’nde tarım ağırlıklı dersleri izledi.1847’de rahip olan ve kısa süre bir hastanede görev alan Mendel, daha sonra 1849’da Brünn yakınlarındaki Znaim’de bir okula yedek öğretmen olarak atandı.Bu yeni işini sevmiş , ders verme hakkını kazanarak doğa bilimleri öğretmeni olmaya karar vermişti.1850’de bu amaçla girdiği üniversite sınavlarında jeoloji ve zooloji konularında başarı sağlayamayınca bu şansını yitirdi, ancak manastır yetkililerinin de desteği ile bilgisini artırmak üzere Viyana Üniversitesi’ne gönderildi.1851-1853 arası bu kurumda doğa bilimleri ve botaniğin yanı sıra , kendisine daha sonraki araştırmalarında yararlı olacak istatiksel yöntemler konusunda öğrenim gören Mendel, 1854’te Brünn Teknik Okulu’nda fizik ve doğa tarihi dersleri için yedek öğretmenlik görevine getirildi.1856’da yeniden üniversite sınavlarına girdiyse de yine başarılı olamadı.Bu dönemde başladığı bitki melezleme çalışmalarını 1861’e değin sürdürdü.O yıl manastırın baş rahipliğine atandığından ,zaman ayıramadığı bilimsel araştırmalarını büyük ölçüde azaltarak manastırı dini vakıflara daha çok katkıda bulunmaya zorlayan bir yasa nedeniyle yerel hükümetle ve eğitim bakanlığı ile uzun yıllarını alacak bir mücadeleye giren mendel, bu dönemde bir yandan manastırın yönetimi ile, bir yandan da 1876’da yönetim kuruluna atandığı bir Maravya bankasının işleri ile uğraştı.

Hücre Bölünmesinin Nedeni ve Amacı Nedir?

Hücre Bölünmesinin Nedeni ve Amacı

Bir hücreden yeni hücrelerin oluşmasına hücre bölünmesi denir. Hücre bölünmesi bütün canlılarda görülen bir olaydır.  Hücre bölünmesi hücre çekirdeğinde başlar ve birbirini takip eden evrelerden (safhalardan) oluşur. Yoğurdun mayalanması, bitkilerin büyümesi, tohumun çimlenmesi, yaraların iyileşmesi, büyüme ve gelişme olayları hücre bölünmesi sayesinde gerçekleşir.  Hücre bölünmesi; mitoz bölünme ve mayoz bölünme olarak iki çeşittir.  a) Hücre Bölünmesinin Nedeni :  Hücrelerde yaşamsal faaliyetlerin sürdürülebilmesi için yapım (özümleme) ve yıkım (yadımlama) olaylarının yani metabolik faaliyetlerin gerçekleşmesi gerekir. Hücrelerin yaşamsal faaliyetlerini sürdürebilmesi için enerji gerekir ve bu enerjide besinlerden oksijen gazı sayesinde elde edilir. (Besin ve oksijen gereklidir). Hücredeki yaşamsal faaliyetler sonucu da zararlı ve atık maddeler (su, CO2, NH3, madensel tuzlar gibi) oluşur. Hücre içine besin ve oksijenin alınmasını ve yaşamsal faaliyetler sonucu oluşan zararlı ve atık maddelerin hücre dışına atılması hücre zarı sayesinde gerçekleşir.  Hücreler yaşamsal faaliyetlerini sürdürürken sürekli büyür. Hücrenin büyümesi demek hücre zarının, sitoplâzmanın ve çekirdeğin büyümesi demektir. Fakat sitoplâzmanın (hacimce) büyümesi hücre zarının (yüzeyce) büyümesinden daha fazla olur. Bir süre sonra hücre zarından madde giriş – çıkışı zorlaşır ve çekirdeğin yöneteceği alan sınırlı olduğu için çekirdek hücreyi yönetemez. (Yönetmekte güçlük çeker). Bu anda çekirdek bölünme emrini verir ve bölünme emri verildikten sonra hücre bölünmesi engellenemez.  Bütün canlılarda hücre bölünmesi çekirdekte yer alan DNA molekülünün emri ile gerçekleşir. Hücrenin bölünebilmesi için belli bir büyüklüğe (bölünebilme büyüklüğüne) ulaşması gerekir.  b) Hücre Bölünmesinin Amacı :  Hücre bölünmesinin amacı canlılarda üremeyi ve büyümeyi sağlamaktır.  Canlılar hücre sayısına göre tek hücreli ve çok hücreli canlılar olarak iki grupta incelenir.  Tek hücreli canlılarda hücre bölünmesinin amacı (hücre sayısını arttırarak) çoğalmayı (üremeyi) sağlamaktır.  Çok hücreli canlılarda hücre bölünmesinin amacı (hücre sayısını arttırarak) doku, organ ve sistemlerin büyüyüp gelişmesini, yıpranan dokuların onarılmasını, ölen hücrelerin yerine yenilerinin yapılmasını sağlamaktır. Bazı çok hücreli canlılarda sperm ve yumurta hücrelerinin oluşturulması hücre bölünmesi sayesinde sağlanır.  NOT : 1- Hücre bölünmesinin nedeni çekirdek/sitoplâzma oranının veya hacim/yüzey oranının  bozulmasıdır. Hacim (sitoplâzma hacmi) r3 ile, yüzey (hücre zarı) r2 ile orantılı olarak büyür.  2- Hücrede bölünme emri, çekirdekte yer alan DNA molekülü tarafından verilir. DNA’nın emri dışında, kontrolsüz şekilde hücreler bölünürse kanserli dokular oluşur.  3- Hücre, yüzeyi arttırmak, hacmi azaltmak için bölünür.  4- Hücre bölünebilme büyüklüğüne ulaştığında çekirdek bölünme emrini vermezse hücre parçalanır.  5- Çok hücreli canlılarda hücre bölünmesi bazı hücrelerde hızlı, bazı hücrelerde yavaş gerçekleşirken bazı hücrelerde belli bir dönemden (yaştan) sonra hiç bölünmezler. İnsanlarda kan, deri, bağırsak hücreleri hızlı, kas hücreleri yavaş bölünürken sinir ve retina hücreleri de belli bir yaştan sonra hiç bölünmezler.

Mitoz Bölünme Nasıl Yapılır?

Mitoz Bölünme ( Konu Anlatımı)

Hücre bölünmesi tüm canlılarda görülen bir olaydır. Bu olayın amacı hücre bölünmesinin gerçekleştiği canlı veya hücreye bağlı olarak yeni hücreler meydana getirmek, yenilenme ve büyümeyi sağlamaktır. Ayrıca bazı canlılarda yumurta ve sperm gibi eşey hücrelerini oluşturmaktır. Bir hücrenin bölünmesi için önce hücrenin belli bir büyüklüğe ulaşması gerekmektedir. Hücre bölünmesi, bir hücreli canlıların çoğalması, çok hücreli canlıların büyümesi erkek ve dişi eşey hücrelerinin meydana gelmesi için gerekli bir olaydır. Hücre bölünmesi vücut hücrelerinde mitoz, eşey hücrelerini oluşturmak için mayoz olmak üzere iki farklı şekilde gerçekleşir. Hücre mitoz bölünme sırasında üstteki şekilde görüldüğü gibi birbirini takip eden farklı evrelerden geçer Mitoz Bölünme de dikkat edilecek hususlar Tek hücrelilerde çoğalma , çok hücrelilerde büyüme için kullanılır. Yıpranan ve yaralanan hücrelerin iyileşmesi mitoz ile olur. Oluşan hücrelerin Kromozom bilgisi aynıdır. Büyüme sırasında mitoz bölünme hızlıdır. Sinir, Sperm ve Yumurta hücrelerinde mitoz bölünme olmaz. Bu evreler sırasında; ( Mitoz Evrelerinin Oluşum Sırası Önemlidir) *Çekirdeğin ve sitoplazmanın bölünmesiyle iki yavru hücre oluşur. *Hücre bölünmesi öncesinde çekirdekte bulunan ve canlının kalıtsal özelliklerini taşıyan maddenin (kalıtım maddesi) birer kopyası yapılır. *Bu kalıtım maddesi mitozun başlangıcında kromozom adi verilen yapılara dönüşür. *Mitozun ilk evresinde kromozomlar belirgin halde görülmeye baslar. *Daha sonraki evrelerde hücrenin ortasında dizilen kromozomlar, hücrenin karşılıklı kutuplarına doğru hareket eder. *Böylece oluşacak hücrelerin ikisi de kromozomların, dolayısıyla kalıtım maddesinin birer kopyasını almış olur. *Bu şekilde çekirdek bölünmesini tamamlayan hücre, sitoplazma bölünmesine geçer. *Sitoplazma bölünmesi sırasında hayvan hücresi  ortadan ikiye boğumlanır ve mitoz bölünme tamamlanır. Bitki hücresinde ise hücrenin ortasında ara lamel adi verilen bir yapı oluşarak hücre ikiye bölünür. Mitoz bölünmede, ana hücreden iki yavru hücre oluşur. Oluşan bu hücreler ana hücre ile ayni sayı ve özellikteki kromozomları içerir. Vücut hücreleri anne ve babadan gelen kromozom çiftlerine sahiptir. Bir takim halinde kromozom içeren hücreler "n" ile gösterilir. Bir takim (n) anneden, bir takim (n) babadan gelmek üzere iki takim kromozom bulunduran hücreler ise "2n" ile gösterilir. Örneğin insanların vücut hücrelerinin kromozom sayısı2n=46'dir. Öyleyse insanların vücut hücrelerinde 23 çift kromozom olduğunu söyleyebiliriz. Kromozom sayıları ile canlıların büyüklüğü ve gelişmişliği arasında bir ilişki yoktur. Tablodaki bilgilerden yola çıkarak kromozom sayıları fazla olan canlıların, örneğin kromozom sayısı 94 olan deniz yıldızının insandan daha gelişmiş olduğunu söyleyemeyiz.

Havasız Ortamda Kaldırma Kuvveti

Şekil – I de hava ortamında eşit kollu terazinin kollarına asılarak hacimleri farklı cisimler dengeleniyor. Hava boşaltıldığında terazi Şekil – II deki durumu alıyor. Çünkü hava ortamında, hacmi büyük olan cisme daha fazla kaldırma kuvveti uygulanır. Hava dışarı alındığında bu kuvvet ortadan kalktığı için hacmi büyük olan cisim aşağı iner.
Eğer havasız ortamda aynı terazi dengelendikten sonra hava ortamına çıkarılsaydı, bu durumda da hacmi büyük olan cisim yukarı kalkardı.